Innehållsförteckning

• Vad är ett punktdiagram?
• Hur skapar man ett punktdiagram?
• Finns det ytterligare alternativ när man skapar ett punktdiagram?
  • Färgdiagram
  • En tredje, kategorisk variabel
  • Numerisk tredje variabel
• Hur används ett bubbeldiagram?
  • Skalenliga bubblor
  • Begränsa antalet bubblor
  • Använd en förklaring till ditt bubbeldiagram
  • Presentera en hypotes
• Avslutande diagram

För den som vill ha ett underlag för att hänga med i artikeln, kan trycka här! Obs: denna data är fabricerad/simulerad. 

---

Punktdiagram eller spridningsdiagram (engelska scatter plot) använder punkter för att representera numeriska värden för två olika variabler, för att se ett eventuellt samband mellan de två. Ett bubbeldiagram kan man säga är en utökning av punktdiagrammet och används istället för att undersöka sambandet mellan tre variabler.

Det här inlägget kommer bl a redogöra för när man bör använda de två, hur man ska tolka dem och olika alternativ till de båda diagrammen.

Vad är ett punktdiagram?

Ett punktdiagram visualiserar ett eventuellt samband mellan två variabler. Diagrammet använder punkter för att representera numeriska värden för de båda variablerna. Värdena för varje enskild datapunkt, indikeras av dess läge på y- respektive x-axeln i diagrammet.

Den vanligaste användningen av punktdiagram är för identifiering av korrelationssamband. Man vill veta om man för ett givet värde på x-axeln, kan återge en bra förutsägelse för ett ungefärligt värde på y-axeln. Ofta är den oberoende variabeln på x-axeln och den beroende variabeln på y-axeln. Relationen variablerna emellan beskrivs sedan som negativa, positiva, starka, svaga, linjära osv. Mer om det senare.

Ett klassiskt exempel är ett punktdiagram som visar förhållandet mellan variabeln längd (x-axeln) och vikt (y-axeln).

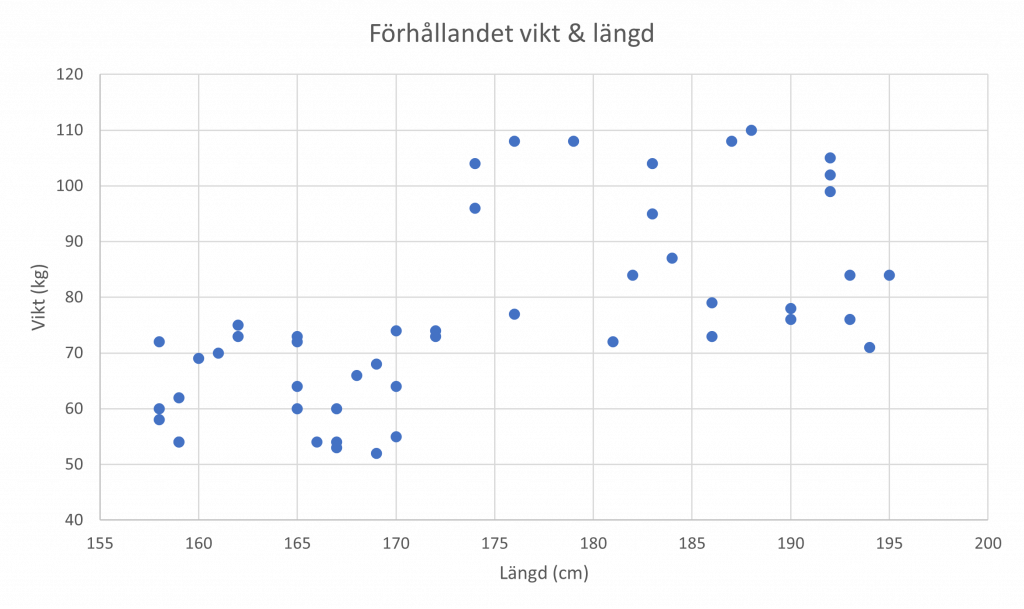
Exemplet ovan visar alltså sambandet mellan längd och vikt. Det verkar som att för ett högt värde på x-axeln, är ens bästa chansning ett högt värde på y-axeln och vice versa. Vill man ytterligare visualisera detta, kan man göra det genom att lägga till en trendlinje.

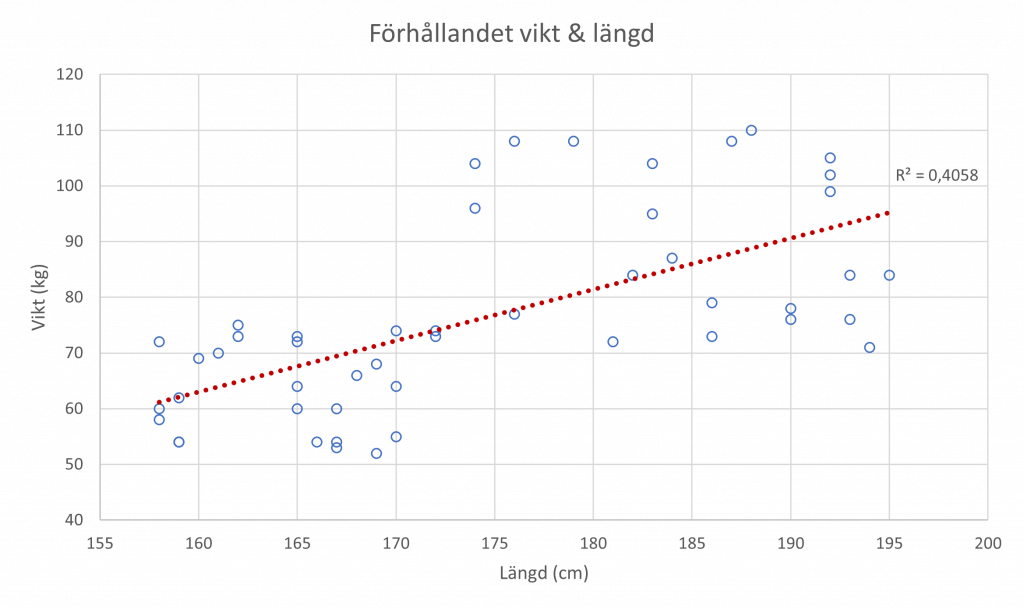
Här syns också det så kallade R-kvadratvärdet. Detta är ett mått på korrelationen mellan variablerna. Kortfattat kan man säga att korrelationen anger styrkan och riktningen av ett samband. I det här fallet med längd och vikt, rör det sig en positiv korrelation. Hade trendlinjen istället lutat nedåt, hade det istället varit en negativ korrelation.

Hur tolkar man ett R-kvadratvärde ungefär lika med 0,41? Som en ganska måttlig positiv korrelation. Viktigt att komma ihåg också är att korrelationen används endast för att undersöka samband mellan variablerna. Kausalitet är ett annat begrepp som innebär att förändring i den ena variabeln, orsakar förändring i den andra. Kanske är så fallet här, men i datamaterialet finns också variabeln ’Kön’, och därför kan ingenting sägas om kausaliteten i det här fallet. Korrelation innebär inte orsakssamband. Behöver man fastställa ett orsakssamband, måste ytterligare analys utföras för att ta hänsyn till eventuella andra variablers effekter.

Man kan även identifiera andra mönster i data med punktdiagram. Man kan dela in grupper av närliggande punkter i så kallade kluster med avseende på deras position. Det går även att använda punktdiagram för att identifiera luckor i datamängden eller för att identifiera extremvärden, värden som ligger väldigt långt ifrån kluster av andra punkter, och som kanske inte följer den generella trenden.

Hur skapar man ett punktdiagram i Excel?

För att återskapa diagrammen ovan, bör man använda bifogad fil. Infoga sedan ett tomt punktdiagram och högerklicka i det tomma diagrammet och välj ’Markera data’. Tryck på ’Lägg till’ under ’Förklaringsposter’ och välj sedan intervallet för längd som ’Värden för X-serie’ och vikt som ’Värden för Y-serie’. Fyll i ett godtyckligt serienamn och tryck ’OK’.

 

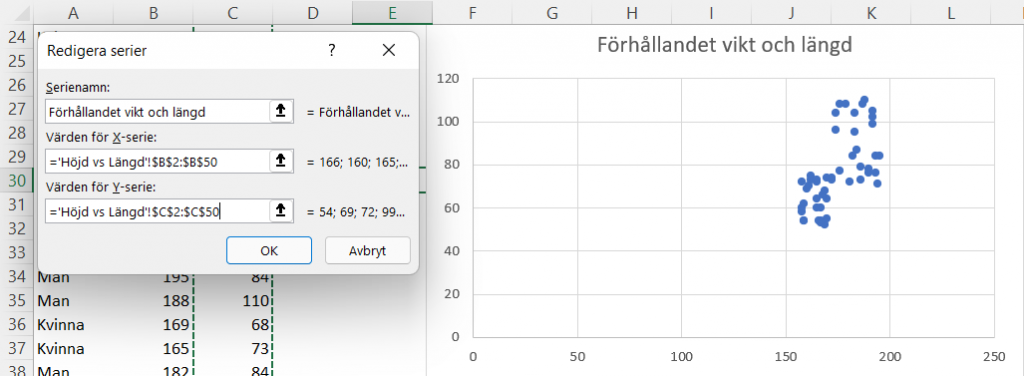
Vad man sedan bör göra är att trycka på x-axeln, högerklicka och sedan välja ’Formatera axel’. Under ’Gränser’ fyll i värdet 155 som minimum, respektive 200 som maximum. Formatera sedan y-axeln på samma sätt.

Vill man lägga till en trendlinje gör man det genom att trycka på det lilla plustecken som dyker upp utanför diagrammets högra hörn när man för muspekaren över diagrammet. Sedan lägger man till R-kvadratvärdet genom att markera trendlinjen, högerklicka och välj ’Formatera trendlinje’. Letar man sig ända ner i formateringsmenyn, finns en ruta för ’Visa R-kvadratvärde i diagrammet’.

Finns det ytterligare alternativ när man skapar ett punktdiagram?

Har man väldigt många datapunkter, kan man råka ut för overplotting. Detta uppkommer då datapunkterna överlappar varandra i hög grad, på ett litet område. En väg runt detta problem är att ta ett slumpmässigt urval av punkter. Tar man ett tillräckligt urval, kommer detta fungera som en bra representation av övriga datamängden. Något man även kan göra är att göra punkterna transparenta, utan fyllning precis som i exemplet ovan, göra dem mindre eller en kombo av alltihop om så krävs.

Färgdiagram

Ett tredje alternativ är att använda ett helt annat diagram, nämligen ett färgdiagram (engelska heatmap). Där representeras varje färg av kluster av punkter.

Ett färgdiagram kan användas vid overplotting, men kan även användas då man vill undersöka ett samband mellan variabler där en eller båda variablerna inte är kontinuerliga (en variabel som inte är uppräknelig, enkelt uttryckt) och numeriska.

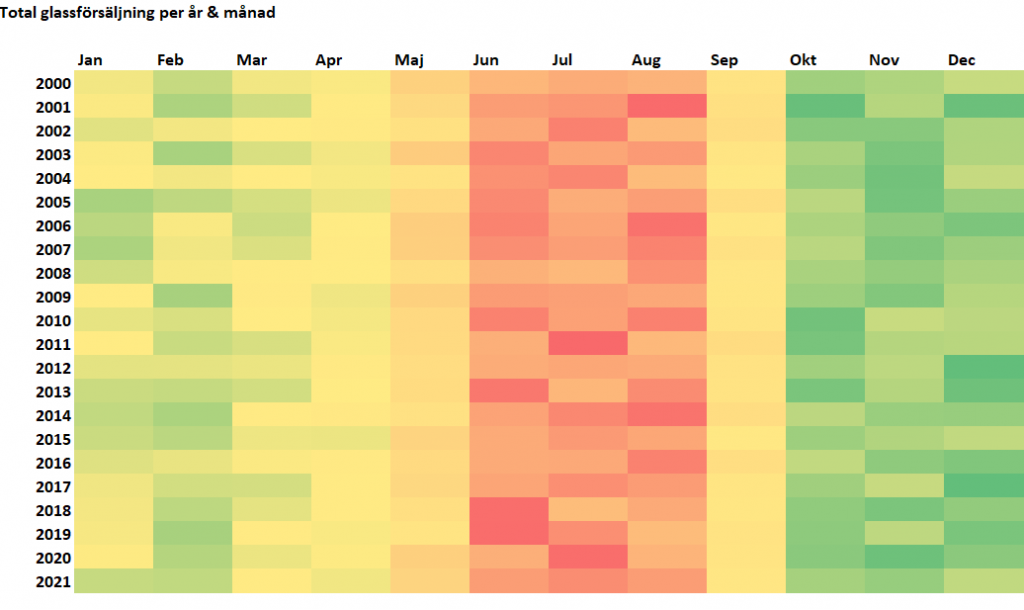
Här representerar den orange/röda färgskalan högre försäljningssiffror, och gul/grönt representerar lägre siffror. Notera att det alltså bara är försäljningssiffrorna som är en numerisk variabel.

En tredje, kategorisk variabel

En annan twist man kan göra är att addera en kategorisk variabel. För att särskilja vad som är vad, kan man formatera punkterna så att de förslagsvis har olika färger. I det tidigare exemplet med längd och vikt, återfinns också variabeln kön. Detta är en kategorisk variabel till skillnad från de två andra numeriska variablerna. Man kan då visa skillnaden mellan könen på det här sättet:

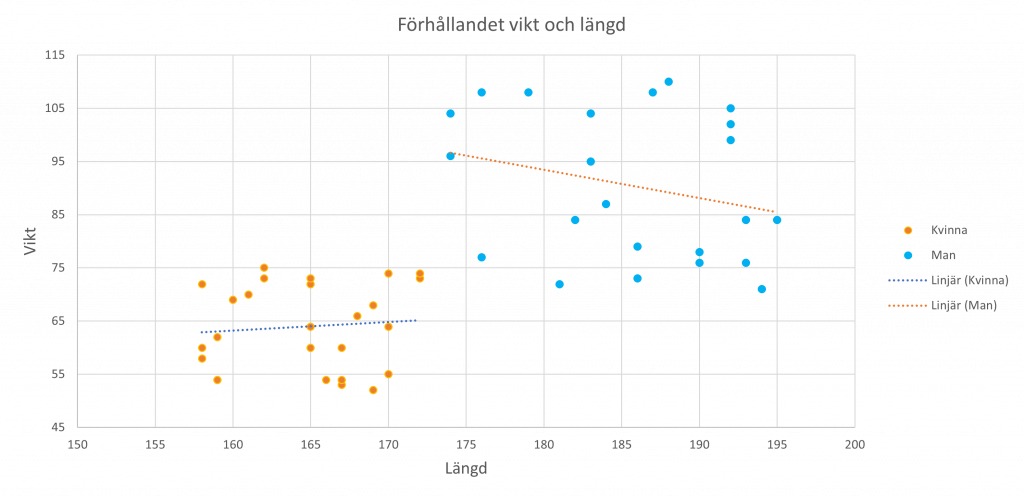
Här ser man enkelt skillnaden mellan könen. Vi ser bl a det verkar vara lite större spridning bland männen.

Numerisk tredje variabel (bubbeldiagram)

Adderar man en tredje variabel till punktdiagrammet, kommer punktdiagrammet byta namn till bubbeldiagram. Punktstorleken kommer även att variera – mindre bubblor representerar lägre värden och större bubblor representerar högre värden. Bubbeldiagram används alltså för att undersöka sambandet mellan tre olika variabler, och variablernas värden indikeras av horisontell position, vertikal position och bubbelstorlek.

Hur används ett bubbeldiagram?

Då bubbelstorleken tillför ytterligare en dimension jämfört med punktdiagram, skulle det krävas flera stycken spridningsdiagram för att visualisera samma sak. Har vi tre variabler X, Y, Z måste man först jämföra X–Y, X–Z, osv. Även om det kan ha sina fördelar, är det i omständligt och tidskrävande. Med ett bubbeldiagram får man istället svaret direkt. Däremot är det några saker man bör eller kan tänka på när man gör ett bubbeldiagram.

Skalenliga bubblor

Tänk på att använda rätt variabel för bubbelstorlek och säkerställ att bubblorna är skalenliga. Om storleken på bubblorna ser konstiga ut, är ett snabbt tips att man provar att byta mellan ’Bubblornas yta’ och ’Bubblornas bredd’ i menyn ’Formatera datapunkter’. Det ska dock sägas att detta sällan är ett problem, då Excel allt som oftast fixar det själv. Notera här också att vi har en hel del bubblor som överlappar varandra, varför det kan vara bra att göra bubblorna något transparenta.

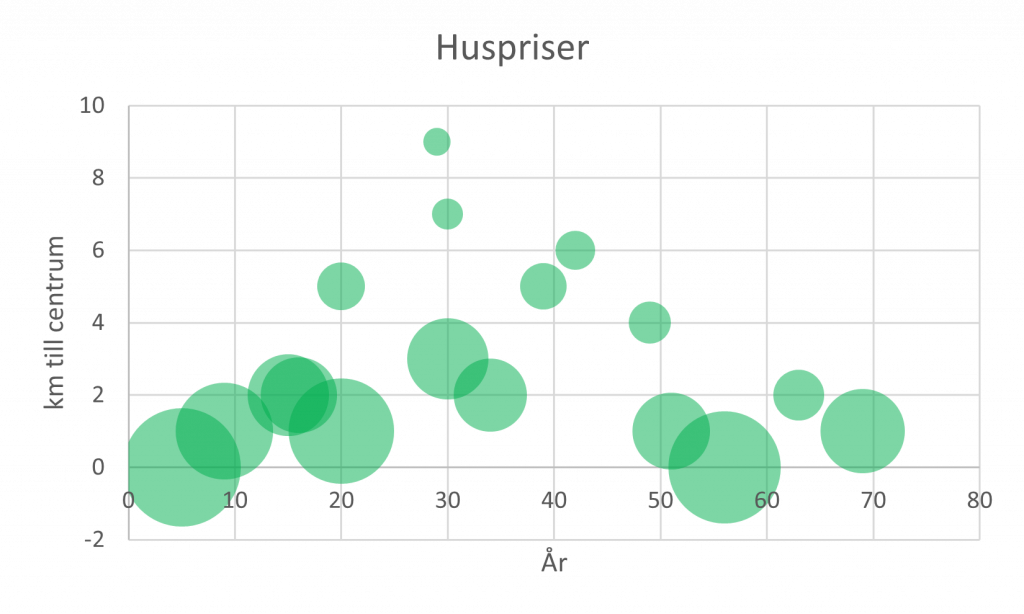
Begränsa antalet bubblor

Här finns det också en stor risk för så kallad overplotting, än större risk än för punktdiagram går nog att hävda. Samma tips gäller även här; gör gärna bubblorna transparenta och har man mycket data, dra ett slumpmässigt urval av datamaterialet. För bubbeldiagram har man även alternativet att skala ned bubblornas storlek, vilket är svårare när det kommer till punktdiagram. Det kan lätt bli plottrigt, speciellt om man vill inkludera dataetiketter som värden eller kategorinamn. Det finns såklart andra urvalsmetoder man kan tillämpa, eller kanske måste tillämpa beroende på vad man har för data eller vad man vill analysera. De metoderna kräver oftast lite mer just i Excel. Det finns ingen tumregel för hur många datapunkter man kan inkludera, men tänk på att diagrammet ska vara läsligt.

Använd en förklaring till ditt bubbeldiagram

Det här är ett ganska generellt tips och gäller nog i de flesta fall, oavsett diagramtyp. Det är särskilt bra när det kommer till bubbeldiagram, då det med en snabb överblick ofta inte är lika lätt att tolka som ett stapel- eller linjediagram.

Här går det också att få en förklaring med respektive skalor, nedskalade. Detta kräver dock lite mera jobb. Man kan även lägga till dataetiketter om man har få punkter.

Presentera en hypotes

Liksom punktdiagrammet är det oftast en hypotes rörande trend eller korrelation man vill presentera. Säkerställ att bubbeldiagrammet är rätt val för att visualisera denna eventuella trend med punktstorlek som en värdeindikator.

När du utvecklar ditt diagram, prova att experimentera med hur variablerna plottas. De två viktigaste variablerna, eller det viktigaste sambandet, bör finnas på respektive axel. Om inte den tredje variabeln bidrar nämnvärt till historien, bör man inte använda bubbeldiagrammet.

 

Avslutande ord

Jag hoppas jag har inbringat lite klarhet i vad de olika diagramtyperna är för något, hur man använder dem och vad det finns för alternativ. Jag hoppas också att många fått upp ögonen för dessa spridningsdiagram, då jag ofta tycker att de förbi ses. För den som är nyfiken på datavisualisering i Excel, erbjuder vi på Learnesy en kurs i ämnet! Man får bl a lära sig om just punkt- och bubbeldiagram (se nedan!).

/Niklas, Produktutvecklare

“Punktdiagram är bra för att visualisera var datapunkter finns inom ett specifikt område. Det fungerar som ett koordinatsystem och tar in 2 värden för varje punkt, ett för den horisontella placeringen, och ett för den vertikala placeringen. Om datan är ordnad på ett specifikt sätt kan man välja ett punktdiagram med linje för att visa ordningen mellan punkterna.

För att lägga in en till serie i ett diagram, högerklicka på diagrammet och tryck på markera data, eller aktivera diagrammet och gå till fliken diagramdesign, och klicka på markera data. I förklaringsposter till vänster, tryck på lägg till. Namnge serien, markera området som du vill lägga in, i det här fallet en X-serie och Y-serie, och tryck på OK, så läggs värdena in i diagrammet. 

Bubbeldiagram fungerar på samma sätt, men tar in ett tredje värde som bestämmer storleken på bubblan. Det kan vara användbart om man vill förtydliga att ett värde förekommer oftare, eller om värdet är mer eller mindre signifikant. Man kan också lägga till trendlinjer i både punkt- och bubbeldiagram för att förtydliga trender.

I formatinställningarna för trendlinjen kan man också välja att visa R-kvadratvärdet, och linjens ekvation. Trendlinjen är förinställd på att vara linjär, men man kan ändra den till exempelvis en exponentiell eller logaritmisk linje. Ekvationen och R-kvadratvärdet för linjen uppdateras automatiskt. Man kan också rita in en prognos baserat på trendlinjen.”