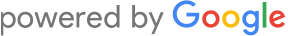Vill man själv prova funktionen SLUTVÄRDE() eller den matematiska formeln, och/eller återskapa diagrammet ovan, så finns en fil för det nedan:

<<Underlag för artikeln>>

Denna artikel behandlar hur man beräknar ränta på ränta i Excel på två olika sätt. Det finns ingen generisk funktion för detta i Excel, man får antingen förlita sig på att skriva en egen formel eller använda sig av funktionen SLUTVÄRDE(). Effekten av ränta på ränta är att man får ränta på den ränta som t ex ett sparande har medfört. Sparandet kan öka i värde både av ränta på kapitalet och som ränta på den tidigare utbetalda räntan.

Ränta på ränta, eller sammansatt ränta, är ränta som beräknas på startvärdet av t ex en investering, plus all tidigare ränta under perioden. Varför man också ibland pratar om kumulativ ränta, alltså ränta på ränta!

Den rent matematiska formeln för ränta på ränta ser ut så här:

där är startvärdet,  är räntesatsen för en viss period (månad, år etc), och är antal perioder.

Exempel på ränta på ränta-effekter är banklån där räntan oftast betalas flera gånger om året. Då årsräntesatsen divideras med antalet perioder per år, får det effekten att den effektiva räntan blir högre än den marknadsförda årsräntan. Ett annat exempel är för investeringar där utdelningar återinvesteras, varför vi får en liknande effekt. Ränta på ränta nämns ofta ihop med snöbollseffekten. Som en snöboll växer och växer för varje gång den rullas i snön, växer kapitalet för varje tidsperiod. Börjar man med en liten snöboll (litet kapital) så tar det ganska lång tid i början för att få den att växa, men allt eftersom kommer den att växa snabbare och snabbare. Låt säga att man 10 000 kr som växer med 10% första året. Det ger en avkastning på 1000 kr. Väljer man att ta den tusenlappen då, kommer pengarna fortsätta växa i samma takt år efter år. Får i stället får avkastningen ligga kvar, kommer man nästa år att få 1100 kr. Vi talar här om en exponentiell tillväxt. Formeln ovan är alltså en exponentialfunktion, något som kommer visualiseras senare.

För att se hur formeln fungerar, kan man sätta in värden i den. Om startvärdet är 10 000, räntesatsen  är 0,10 och antal år är 30, får vi följande:

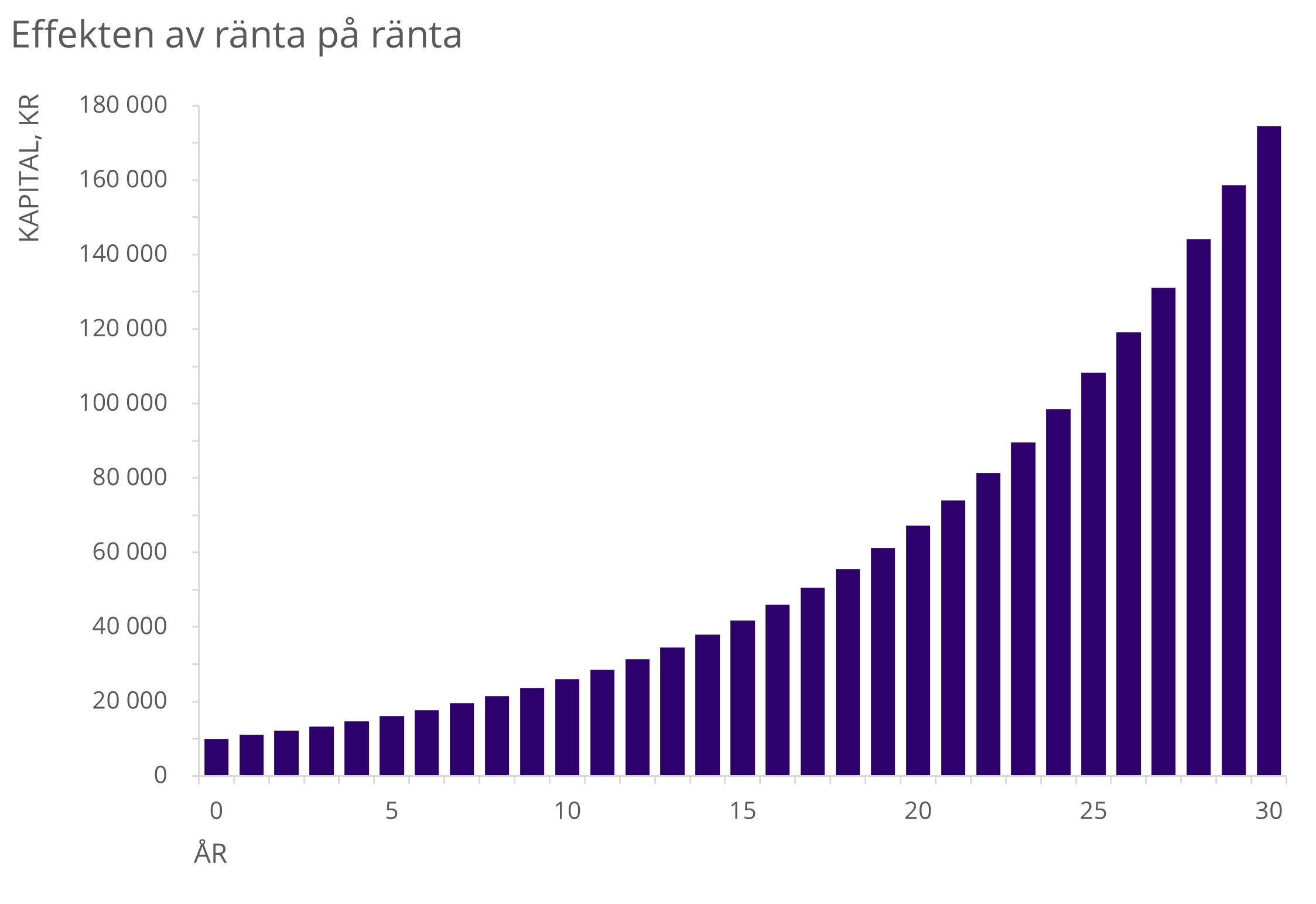
En tidsperiod på 30 år ger följande diagram:

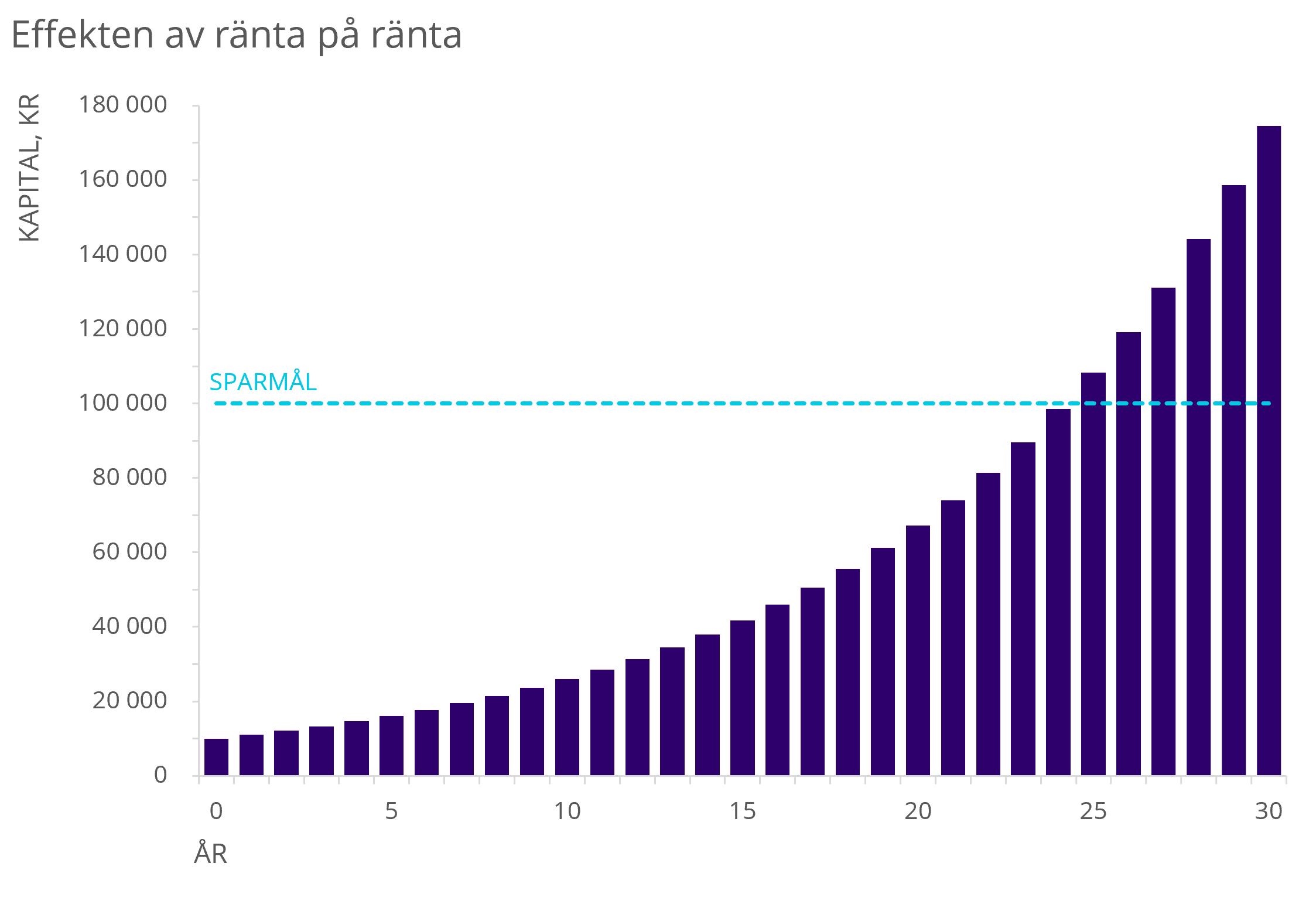
Kurvan är alltså ett bra exempel på den beskrivna snöbollseffekten, dvs kapitalet ökar mer drastiskt för varje år.

Exponentialfunktioner följer de regler som alla andra funktioner lyder under. Dock har exponentialfunktioner sina egna unika sub-regler. Det är en av de viktigaste funktionerna i matematiken, och skiljer sig alltså från den kanske allra viktigaste; den linjära. Kortfattat kan man säga att det är den oberoende variabeln i exponenten ger kurvan sitt utseende.

Har man grafen kan man således lösa ekvationen ”hur många år tar det tills jag har sparat så mycket?”. Detta kan man också lösa rent matematiskt, men det får anses som överkurs.

Den finansiella funktionen SLUTVÄRDE() returnerar det framtida värdet av en investering baserat på en fast räntesats. SLUTVÄRDE() går att använda för fasta, återkommande betalningar eller betalning i klumpsumma.

SLUTVÄRDE() använder sig av tre obligatoriska argument, och två valfria. Denna funktion med dess argument kan användas för att räkna ut den sammansatta räntan. Jag kommer här vissa hur man med fyra av funktionens fem argument kan räkna ut den sammansatta räntan fördelat över 30 år, och utgår från det tidigare exemplet:

Detta överensstämmer med det ”teoretiska” värdet. Funktionen fungerar så här:

Ex.               =SLUTVÄRDE(0,1; 0; 0; -10000)

SLUTVÄRDE(årsräntan; antal perioder där avkastningen på räntan ska adderas, i det här fallet 1, då det är årligen; i det här fallet antal år med start från 0; -10 000kr används då det är investeringen som lämnar plånboken).

Som sagt så finns ingen generisk formell för att beräkna ränta på ränta i Excel. SLUTVÄRDE() används vanligtvis för att beräkna ett låns slutvärde, dvs pengabeloppet man vill vara skyldig efter att alla återbetalningar är gjorda. Detta värde bör vanligtvis och rimligtvis vara 0, eftersom de flesta inte vill dras med någon skuld. Funktionen SLUTVÄRDE() returnerar ett låns slutvärde om vi har de andra relevanta värdena. Därför kan man använda funktionen för att undersöka vilken betalningstakt man bör hålla för att vara skuldfri efter x antal år.

Det bör också sägas att SLUTVÄRDE() kan vara knepigare att använda i exempel där perioder inte är år, utan snarare kvartal eller månader. Det krävs då att man funderar på hur många inbetalningar som man måste göra per år. För månadsvis blir syntaxen ungefär så här:

=SLUTVÄRDE(0,1 / 12; antal år * 12; 0; -10000)

då vi ständigt måste ta i beaktning att det går 12 månader på ett år.

I Excelfunktioner Fördjupning får man lära sig över 90 användbara funktioner. Ett helt kapitel är dock tillägnad finansiella funktioner. Där tas bland andra funktionen SLUTVÄRDE() upp. Likaså finns det en lektion för att beräkna just ränta på-ränta. I lektionen beräknas den sammansatta räntan med en egensnickrad matematisk formel.

”Eftersom det inte finns en inbyggd funktion för det, så kommer denna lektion att visa ett sätt att hantera ränta på ränta. Vi har tagit ett lån på 150,000kr, med en årsränta på 7%.

För att få fram den årliga sammansatta räntan, så skriver vi Lika med, och markerar det originella lånet. Vi kommer nu att behöva multiplicera lånet med räntan, vilket är 1.07. Vi får då fram lånet, plus den 7-procentiga årsräntan. Kopierar vi neråt ser vi den sammansatta räntan för varje år. Det finns en formel för detta, och vi använder värdena nedanför.

Vi skriver in Lika med, markerar lånet, gånger, inom klammer: ett plus Ränta, dividerat på perioderna per år… Upphöjt till, inom klammer, perioderna per år, gånger antalet år. Som vi ser så är värdet vi fått fram samma som i den andra metoden. Om vi sammansätter varje månad, kan vi helt enkelt ändra perioderna per år till tolv… så ser vi att resultatet ändras trots att antalet år förblir desamma. I denna lektion har vi gått igenom hur man hanterar ränta på ränta i Excel”

I lektionen tas ytterligare ett exempel på en situation upp; men för att återgå till det återkommande exemplet för det här inlägget, ska jag beräkna investeringen på 10 000kr efter 30 års tid. Prova gärna denna formel i den övningsfil som tillhör lektionen ovan. Formeln (utan några cellreferenser) blir då: =10000*(1+(0,1/1))^(1*30), vilket resulterar i 174 494kr. Prova gärna att byta ut värdena i cellerna istället. I övningsfilen kan man också passa på att använda SLUTVÄRDE() på samma sätt som jag har gjort i tabellen. Glöm inte att visualisera detta med ett linje- eller stapeldiagram, eller kombinera de två.

Jag hoppas detta inlägg ska hjälpa er att beräkna ränta på ränta. Det är förhållandevis enkelt så länge man vet formeln och / eller använder sig av SLUTVÄRDE(), och framför allt om det är årligen. Man bör också förstå vad sammansatt ränta är för något. Vill man veta mer om vad för kurser Learnesy erbjuder, kan man göra det här.