Att välja mellan linjär och logaritmisk skala kan göra stor skillnad i hur dina data presenteras och tolkas. Men vad är egentligen skillnaden, och när ska du använda vilken? I den här artikeln förklarar vi grunderna och guidar dig genom fördelarna och användningsområdena för båda skalorna – så att du kan skapa tydliga och effektiva visualiseringar varje gång.

Här nedan kan du se en kort lektion på ämnet.

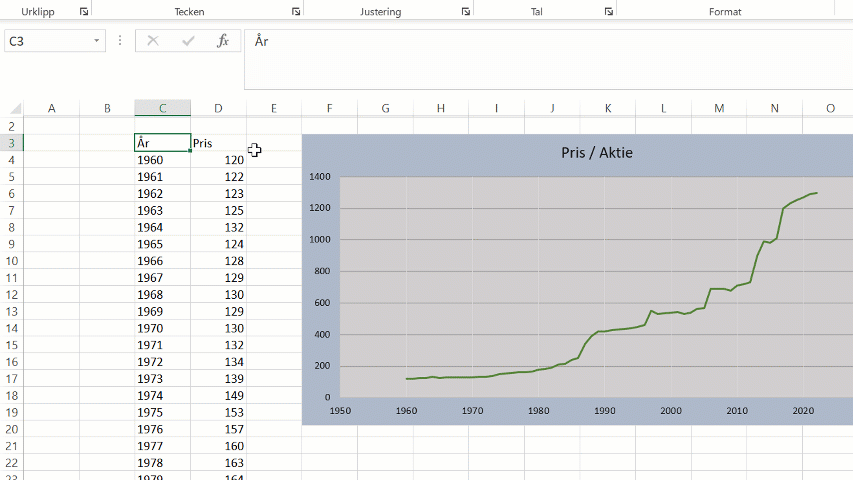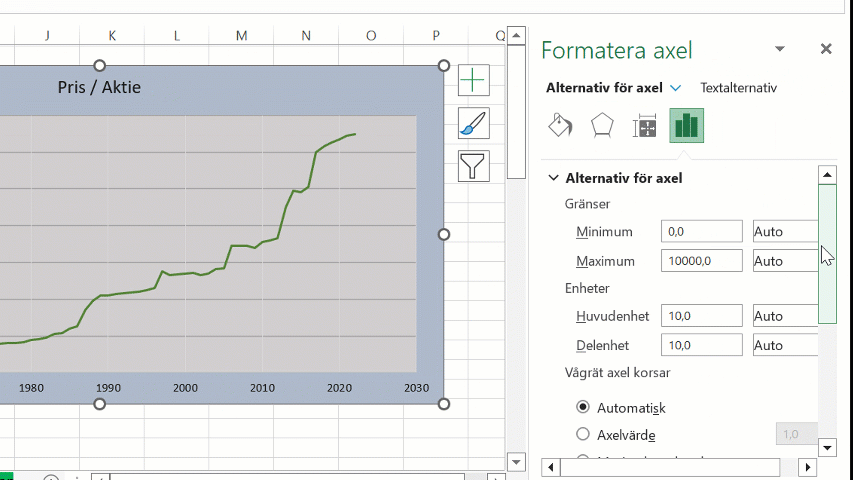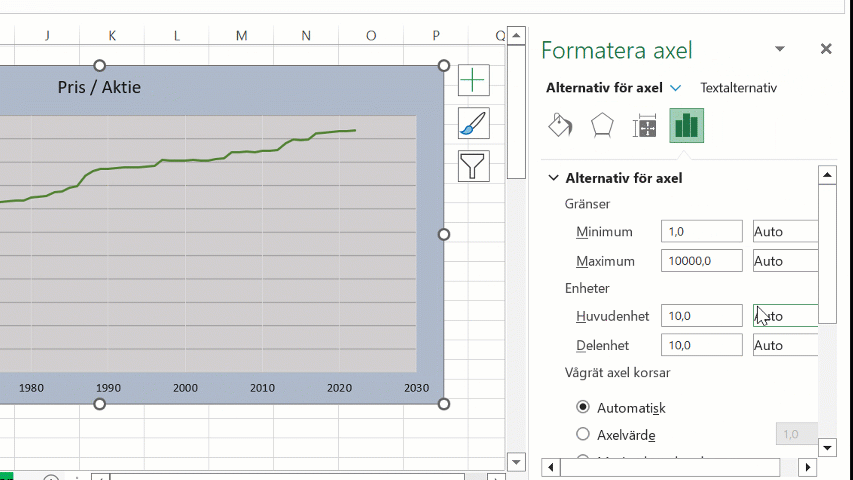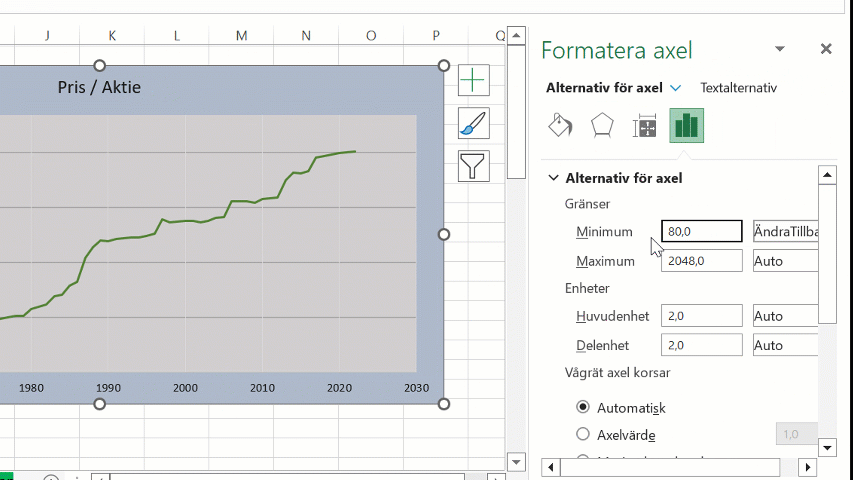
Diagram i Excel ritas per automatik på en linjär skala. En linjär skala är helt enkel en skala, där alla intervall är lika stora. Det finns dock flera fall då linjära skalor inte är att föredra när vi visualiserar data. Vi ska nu se på två fall där en logaritmisk skala visar sig vara användbar. Vi börjar med ett exempel där vi mappar upp ålder mot bruttoinkomst för 100 personer (i form av ett punktdiagram).

Även om man kan anta att inkomst växer i takt med ålder blir det svårt att se i diagrammet, eftersom det finns personer med mångfaldiga inkomster i relation till majoriteten.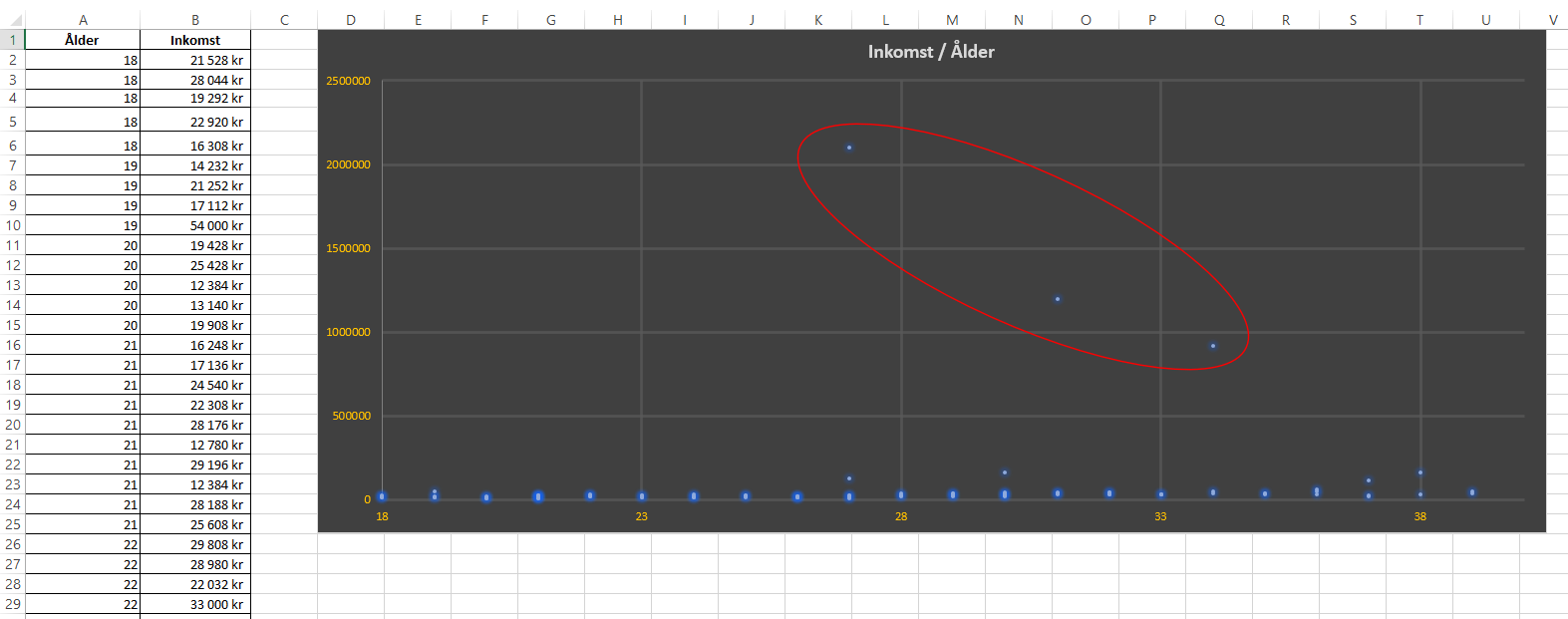

Då varje intervall på y-axeln är lika stor, kommer lägre inkomster att komprimeras i diagrammet efter varje intervall som läggs till för att kunna nå de högsta värdena i dataserien.

Problemet här kan lösas med hjälp av en logaritmisk skala. Till skillnad från linjära skalor, definieras en logaritmisk skala som: föregående intervallvärde multiplicerat med ett basvärde. 

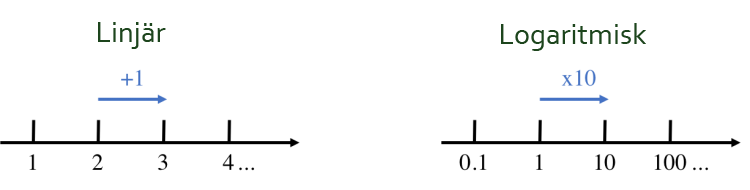
Grundtanken är alltså att vi komprimerar höga värden, för att hålla hög “resolution” bland lägre värden.

>>> För att ändra en axel till logaritmisk i Excel, högerklicka på axeln och välj “Formatera axel“. Klicka sedan “Logaritmisk skala” och skriv in basvärdet.

Vi ser nu att höga inkomster ligger i sitt egna intervall. Bland lägre inkomster ser vi en tydlig trend som tyder på att inkomst ökar i takt med åldern.

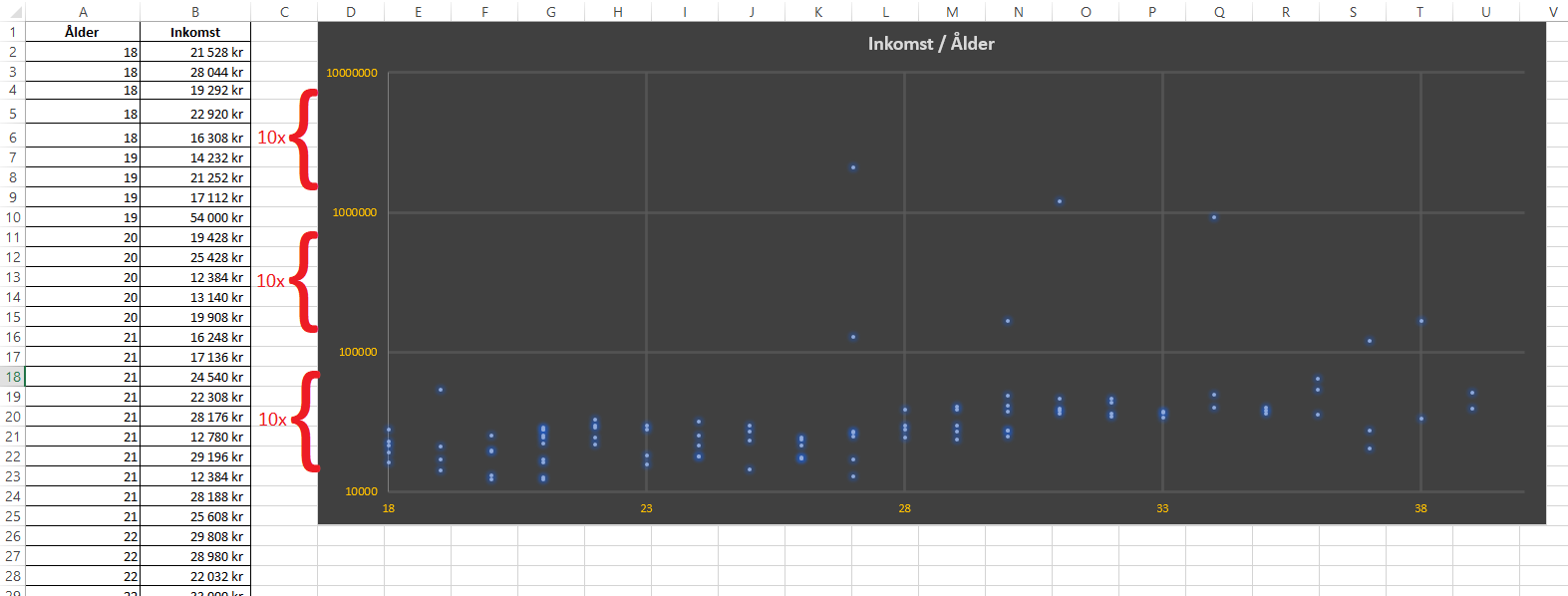
Det finns inte en tydlig regel när vi bör använda oss av en logaritmisk skala, men vanligtvis används de för två skäl. Det första är när stora värden förvränger grafen för data, och den andra är att visa multiplikativa faktorer eller procentuella förändringar.

Vi ser på ett till exempel med procentuell förändring: om vi ändrar basvärdet från 10 till 2, betyder det att varje intervall är en ökning av 100%. Detta är synnerligen användbart om det är den procentuella skillnaden som är av intresse.

Bland annat i ekonomiska sammanhang är det inte ovanligt att betrakta t.ex. marknadsindex eller aktiepriser som procentuella förändringar:

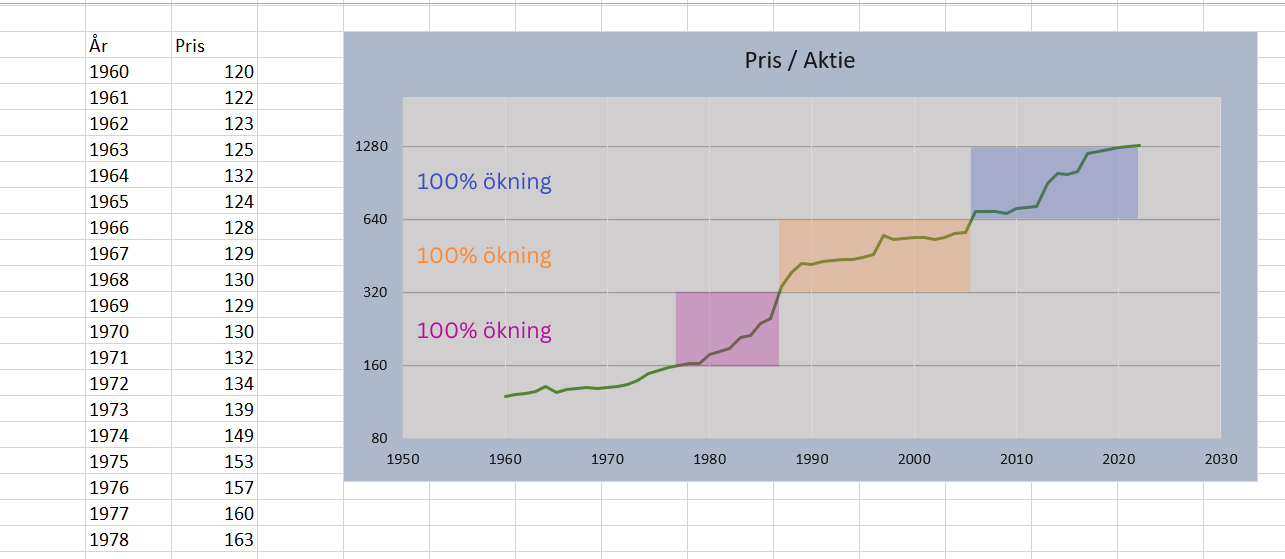
Genom att ställa in ett minimumvärde i diagrammet kan vi även styra vilket grundvärde den logaritmiska skalan baserar sig på: