I ett av våra tidigare inlägg lärde vi oss att lösa den kortaste vägen i Excel med hjälp av problemlösaren. Problemlösaren är ett tillägg i Excel som tillåter oss att optimera linjära matematiska modeller – utan att behöva lösa ekvationer för hand.

I stället är det en modell vi bygger med Excel, som motsvarar våra linjära ekvationer, men där problemlösaren senare bestämmer det optimala värdet för variabler i ekvationen. Med “optimal” menas variabler som antingen minimerar eller maximerar resultatet, eller alternativt ger oss ett resultat som är närmast ett önskat värde.

Följande är ett klassiskt optimeringsproblem som vi ska lösa med hjälp av Excel och problemlösaren:

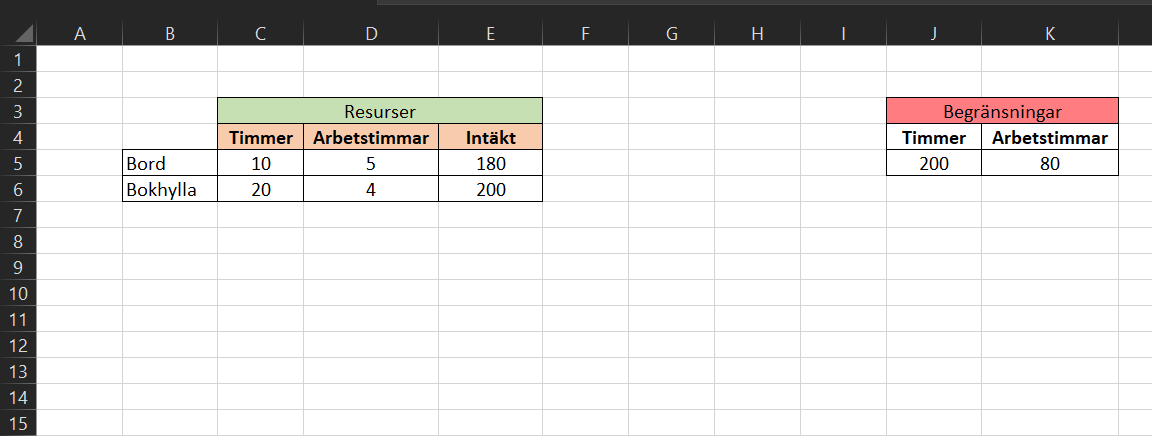
Ett företag vill optimera sin produktionslinje som tillverkar två produkter: bord och bokhyllor.

• För att tillverka ett bord krävs det 10kg timmer och 5 arbetstimmar. Ett bord säljs för 200€
• För att tillverka en bokhylla krävs det 20kg timmer och 4 arbetstimmar. En bokhylla säljs för 180€
• Produktionslinjen har 200kg timmer, och 80 arbetstimmar tillgängligt
• Hur många bord och bokhyllor bör produktionslinjen producera för att maximera vinsten – givet våra begränsningar 200kg timmer och 80 arbetstimmar?

Funktionen vi vill optimera är således:
f(x,y) = 180x + 200y

Alltså summan intäkter från:
180€ * [antal bokhyllor] + 200€ * [antal bord].

Det här är den så kallade objektiva funktionen i problemet ☝️

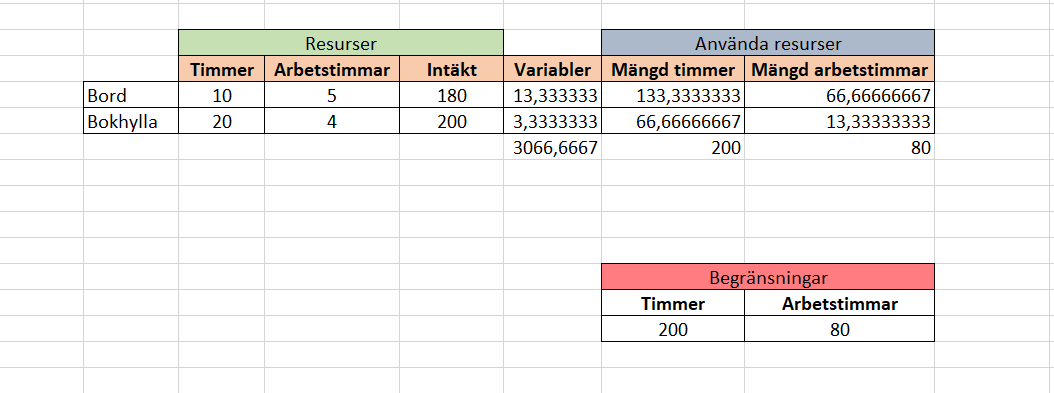
Vi öppnar Excel och börjar med att skapa två tabeller:

• En som innehåller information om resurser (timmer, arbetstimmar & intäkter)
• En tabell som innehåller våra begränsningar (200kg timmer & 80 arbetstimmar)

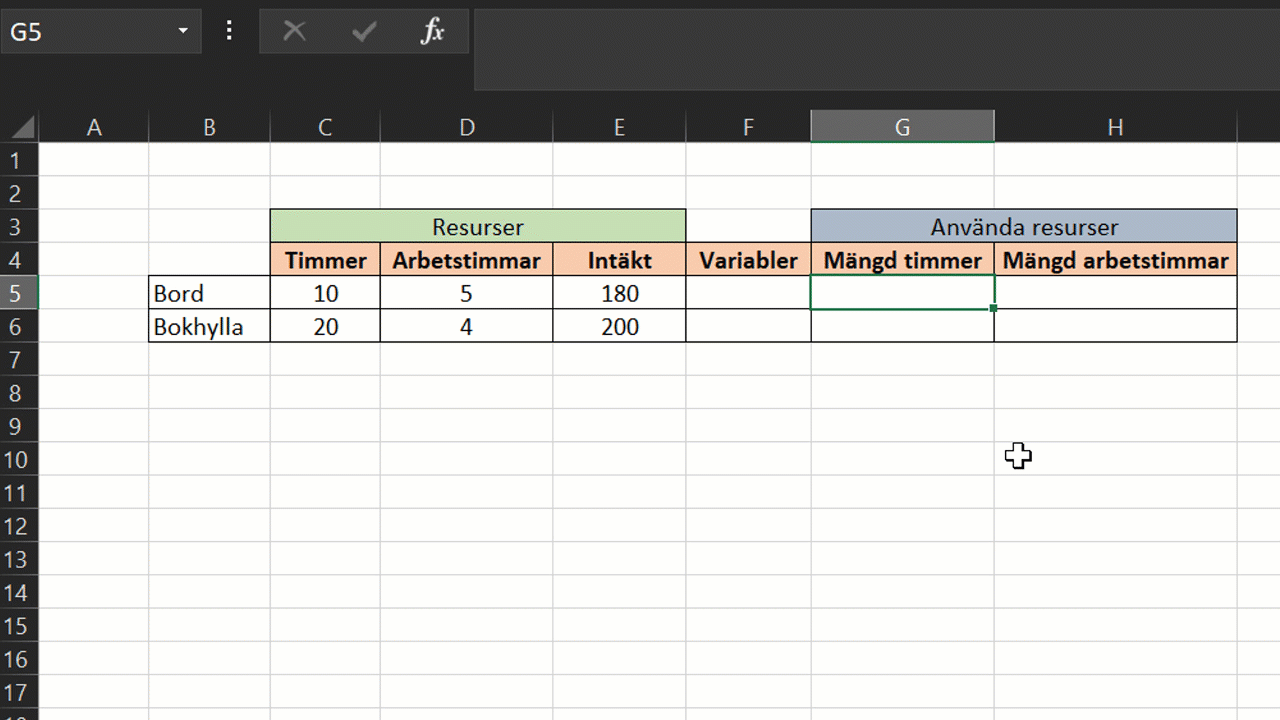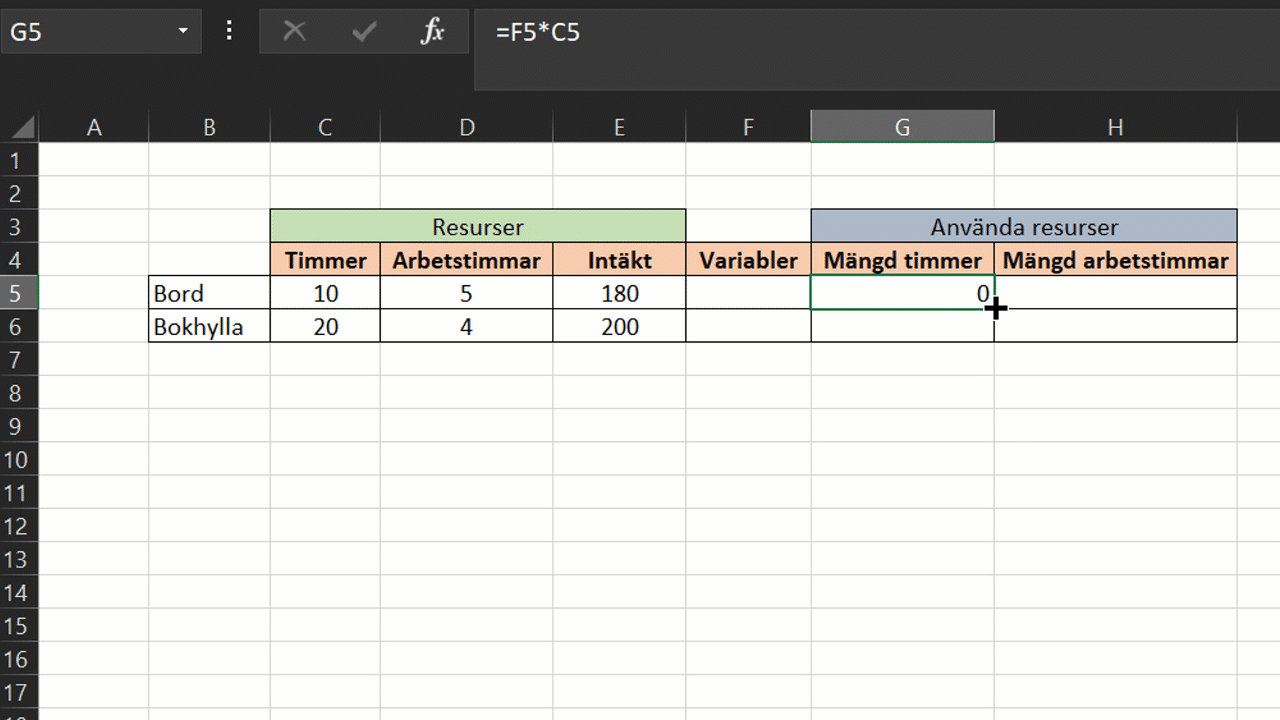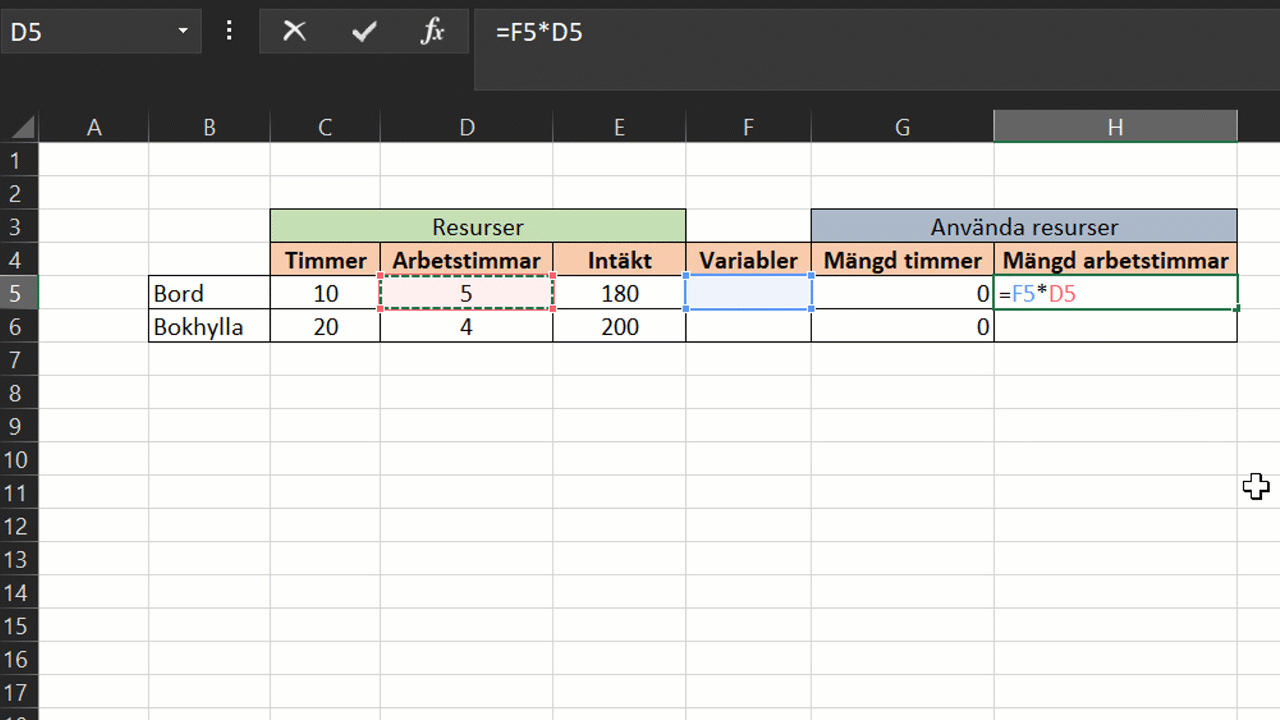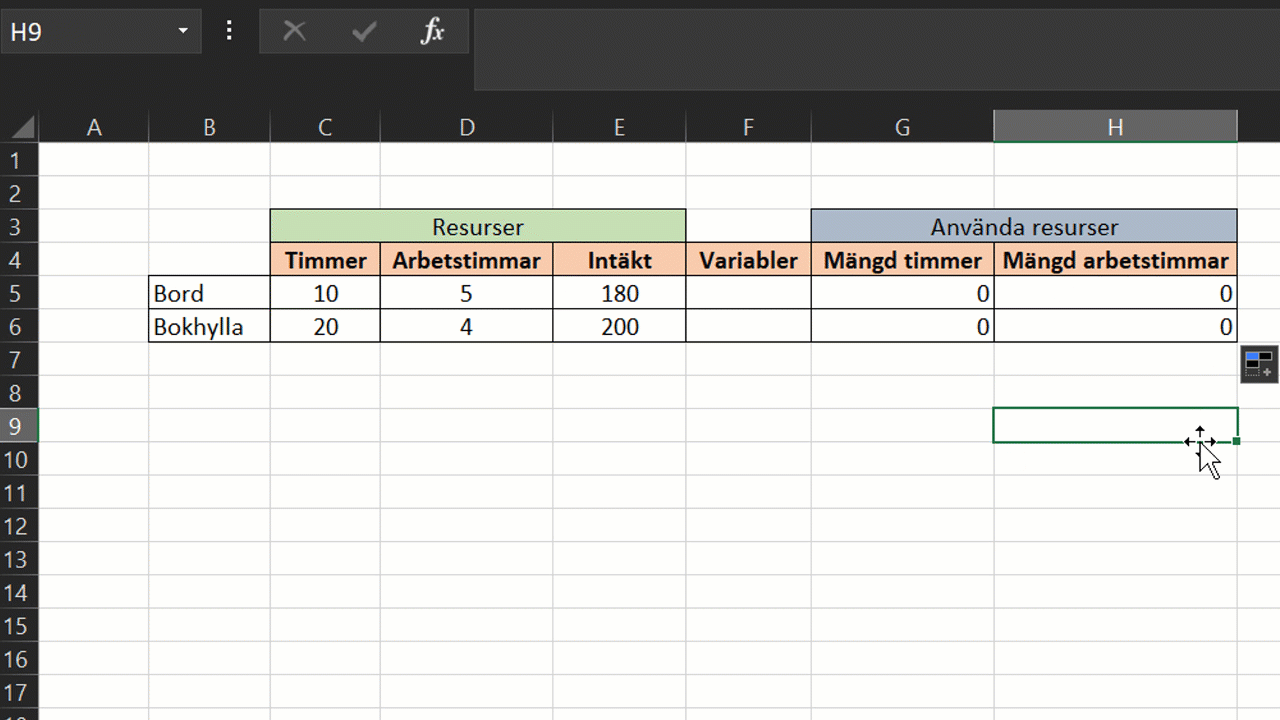
Vi fortsätter med att skapa 3 nya kolumner i tabellen för resurser. Första blir våra variabler x och y, det vill säga mängden bokhyllor och bord som bör produceras för att maximera vinsten på produktionslinjen. Vi låter denna kolumn stå tom för tillfället, eftersom värden för variabler bestäms senare av problemlösaren.

I de två andra kolumnerna räknar vi ut hur mycket timmer och arbetstimmar det går åt för att tillverka x och y mängd av respektive produkt. Vi multiplicerar då variablerna med mängden resurser per produkt.

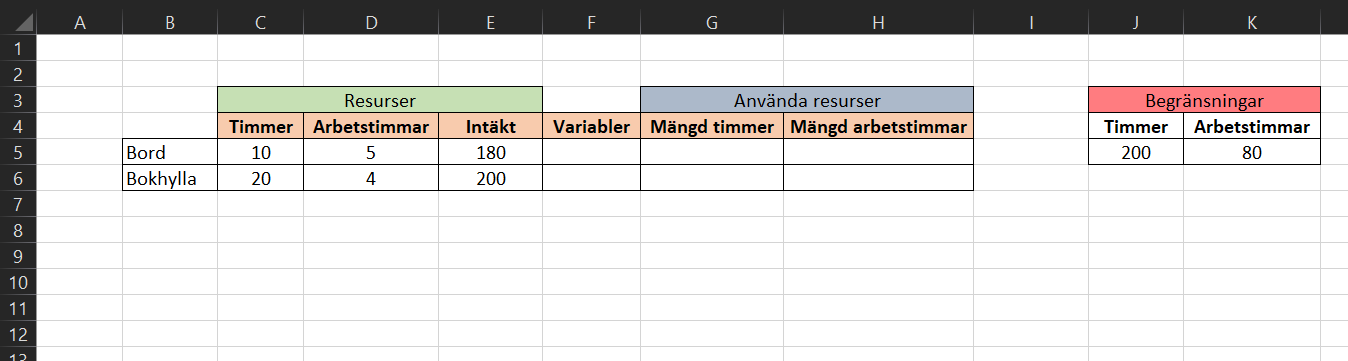
Multiplicera variablerna x och y med timmer och arbetstimmar per produkt.

Testar vi med att fylla i värden för variabler manuellt, till exempel 2 st. bord och 3 st. bokhyllor ser vi hur mycket resurser förbrukas i tillverkningen.

Nu skriver vi in den objektiva funktionen som vi vill maximera, d.v.s. intäkter:
f(x,y) = 180x + 200y

I Excel är detta en PRODUKTSUMMA-funktion med kolumnerna Variabler och Intäkt som argument.

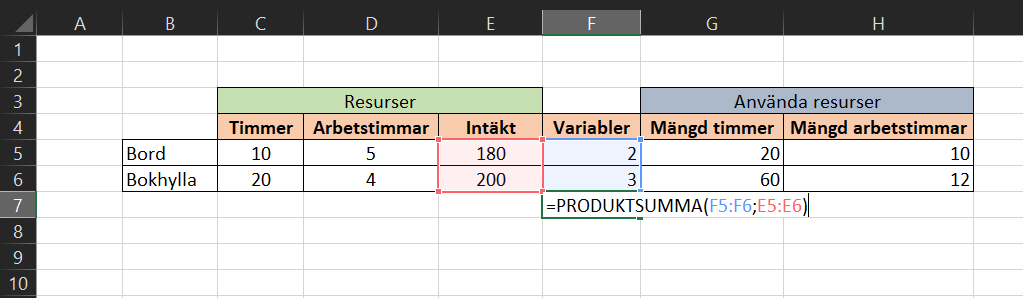
Vi måste även ha en funktioner som ger oss värden vilka motsvarar våra begränsningar. Annars kan inte problemlösaren räkna ut ett optimalt svar.

Då blir sista steget i att lägga till summa-rader som räknar totala mängden timmer och arbetstimmar för x och y, eftersom dessa inte får överskrida 200 eller 80.

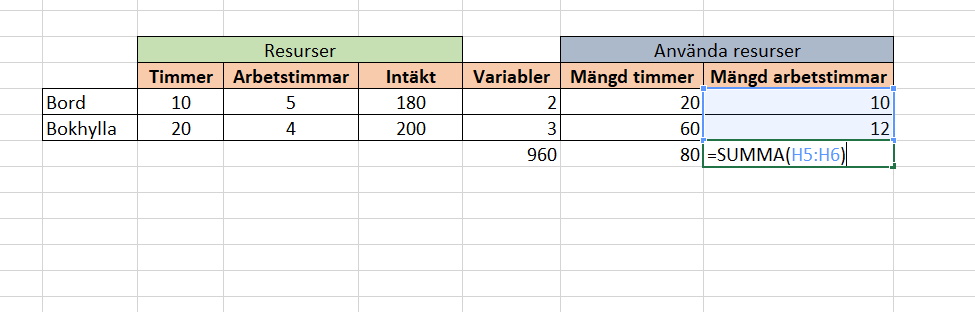
Fortsätt sedan med att radera testvariablerna för x och y från modellen och öppna problemlösaren.

• Ange den objektiva funktionen som målsättning
• Välj “Max” för att räkna ut största möjliga värden för variabler
• Ange x och y som variabla celler (F5 & F6)

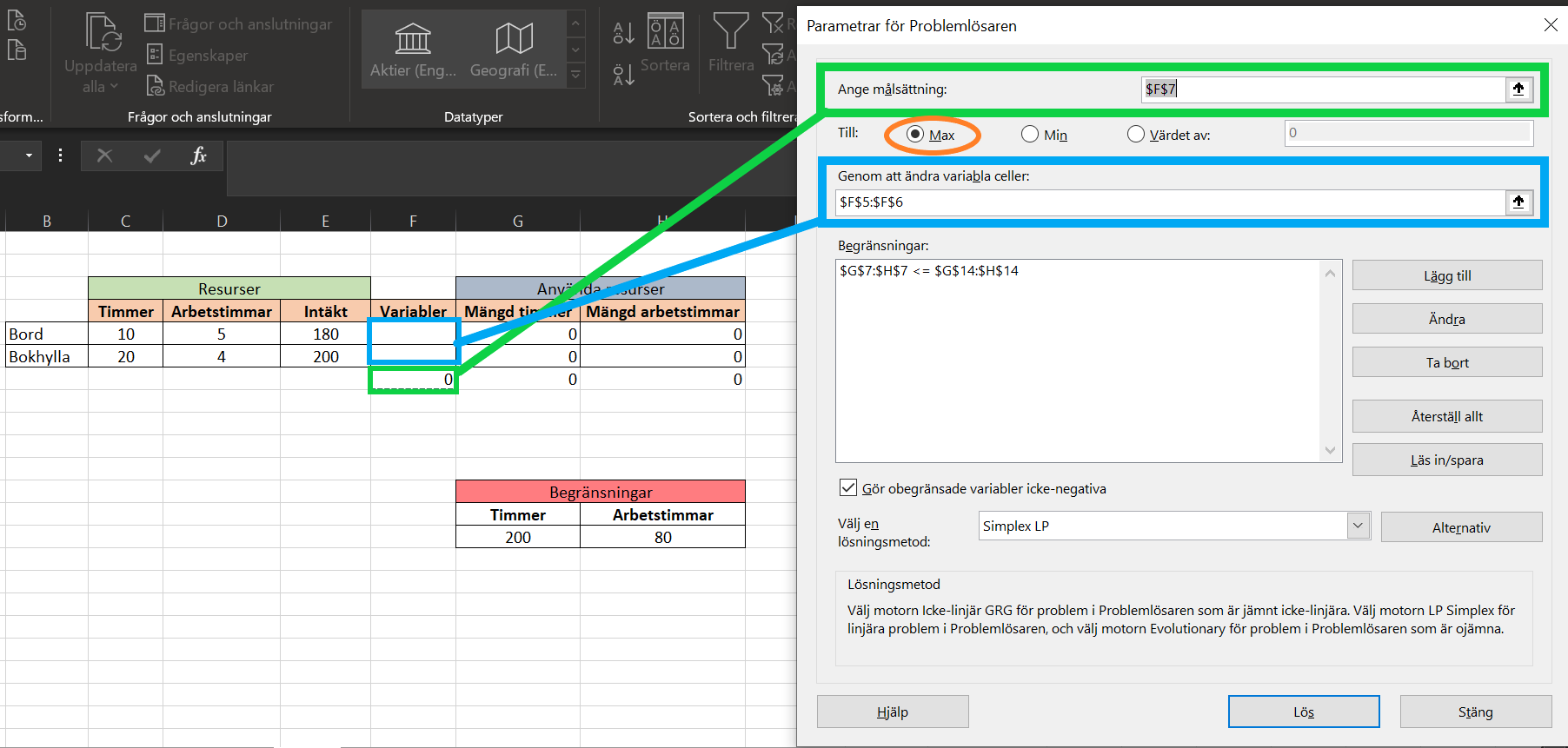
Vad som kvarstår är att förse lösaren med våra begräsningar som är totalsummorna av “mängd timmer” och “mängd arbetstimmar” mindre eller lika med våra värden i begränsningstabellen. Välj sedan Simplex LP som lösningsmetod och klicka på “Lös”.

Vi kan nu se att det optimala svaret på hur många bord och bokhyllor vi bör tillverka för att maximera vinsten är:

• 13,3 bord
• 3,3 bokhyllor
• Vilket ger oss en intäkt på ca. 3066€

Hur vet vi att svaret är rätt?

Ritar vi ut de linjära ekvationerna 5x + 4y = 80 och 10x+ 20y = 200, det vill säga våra begränsningar, får vi följande grafer:

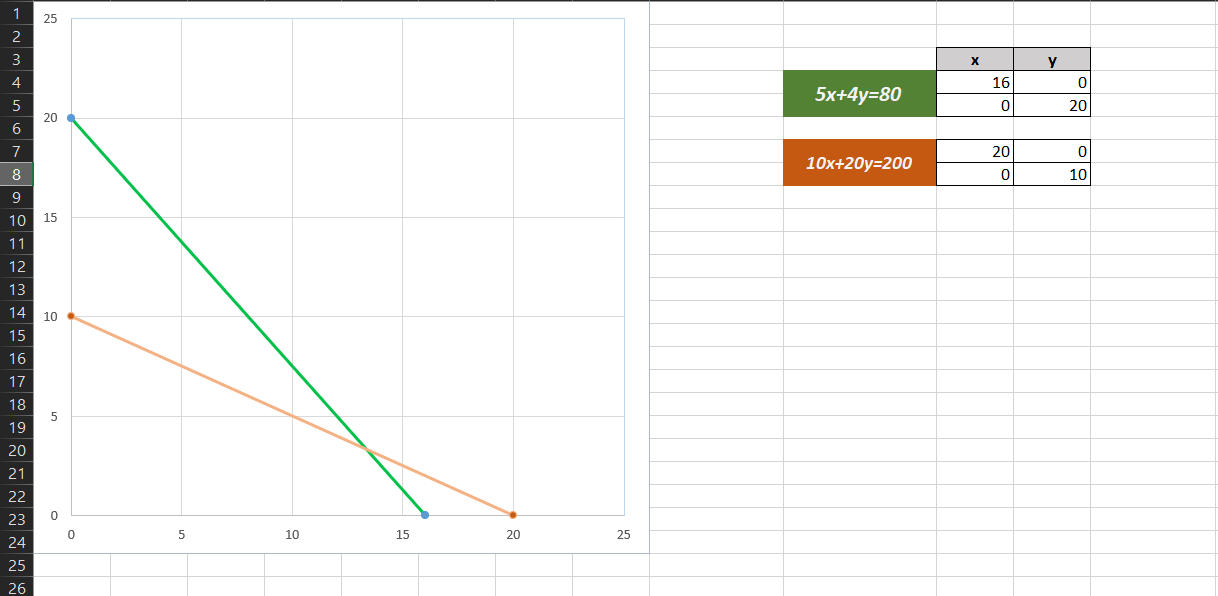
Den gröna linjen visar alla kombinationer av x och y (mängd bokhyllor och bord) som förbrukar alla tillgängliga arbetstimmar – den orange linjen visar det samma för timmer.

Området som begränsas av båda funktionerna kallas det möjliga området. Alla kombinationer av x och y som inte kränker våra begränsningar finns inom detta område.

För att kontrollera om vår lösning är rätt kan vi sätta vår ursprungliga funktion som maximeras f(x,y) = 180x + 200y lika med 3066. Detta ger oss en linje som tangerar ett av hörnen i det möjliga området, vilket är svaret.

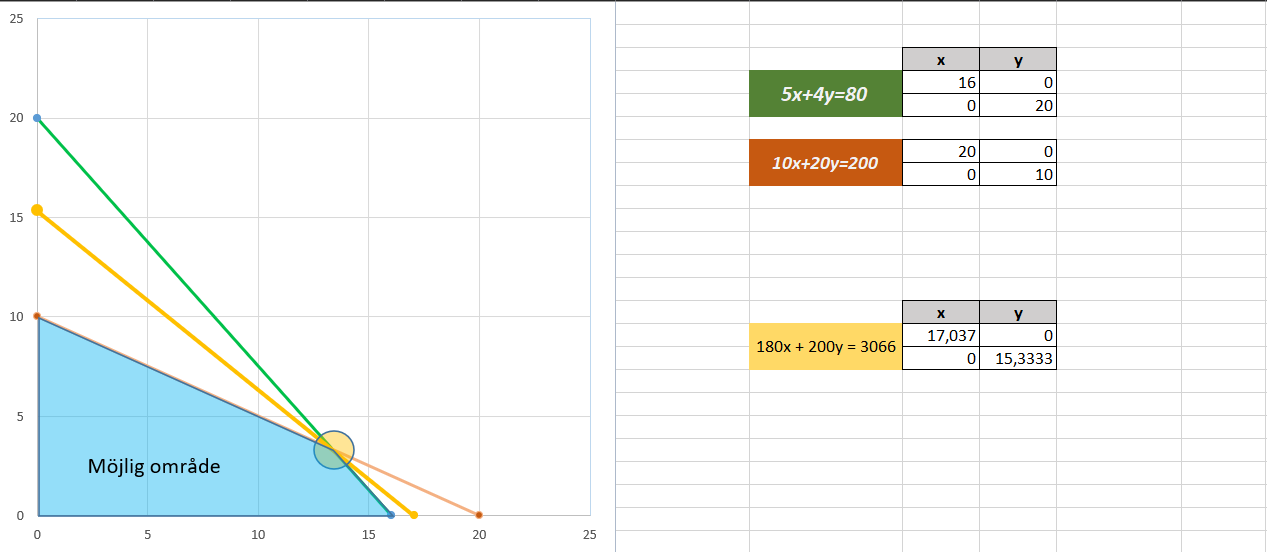
Beroende på funktionen och hur vi vill optimera den, kan linjen tangera olika punkter – men då alltid målet är att maximera eller minimera finns den optimala lösningen i ett av det möjliga områdets hörnpunkter.

Om du är intresserad av vårat utbud av onlinekurser i Excel och Dataanalys, klicka här.