Å velge mellom lineær og logaritmisk skala kan gjøre stor forskjell for hvordan dataene dine presenteres og tolkes. Men hva er egentlig forskjellen, og når bør man bruke hvilken? I denne artikkelen forklarer vi grunnprinsippene og guider deg gjennom fordelene og bruksområdene for begge skalaene – slik at du kan lage tydelige og effektive visualiseringer hver gang.

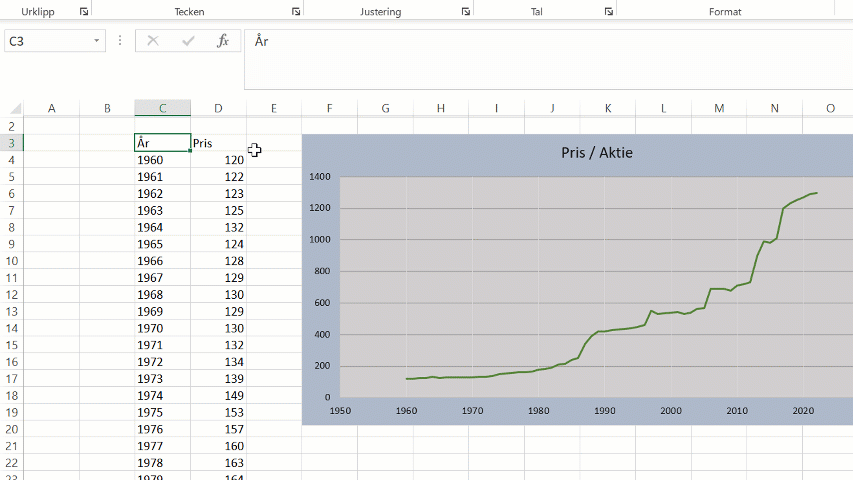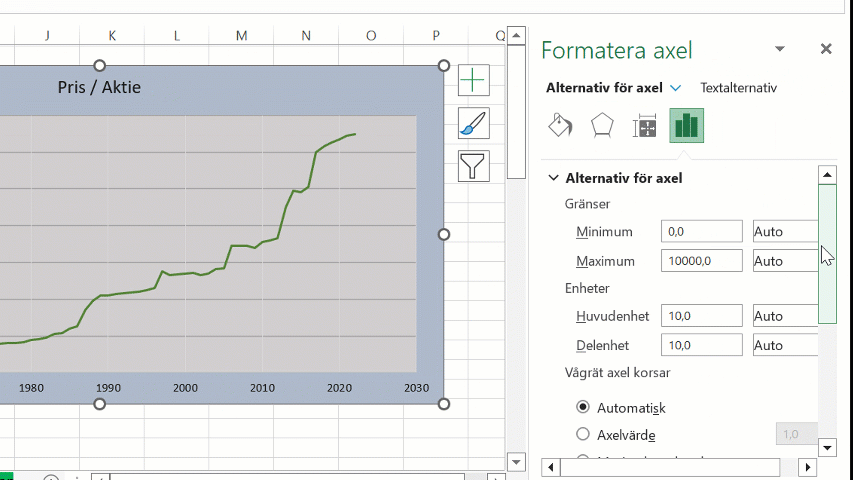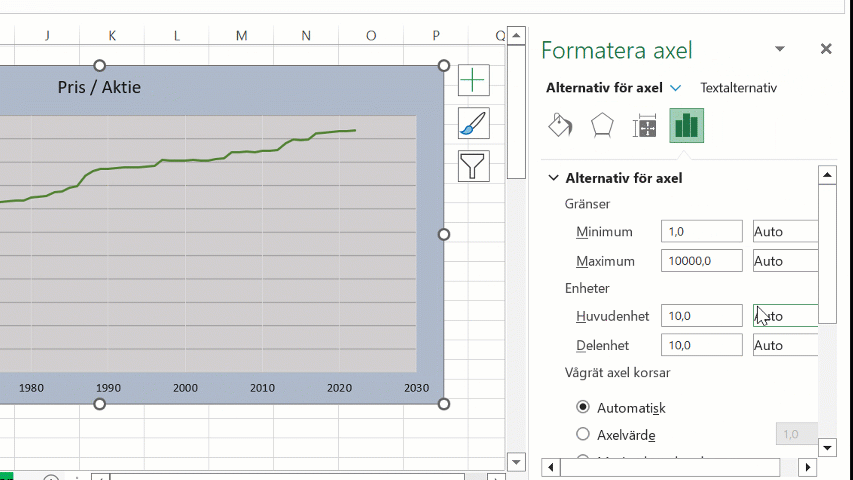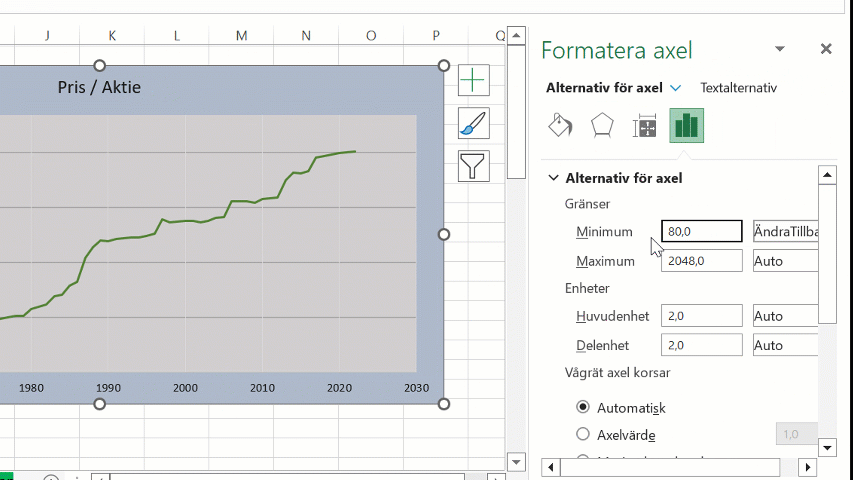
Diagrammer i Excel tegnes automatisk med lineær skala. En lineær skala er rett og slett en skala der alle intervallene er like store. Det finnes imidlertid flere tilfeller der lineære skalaer ikke er ideelle når vi visualiserer data. Vi skal nå se på to situasjoner der en logaritmisk skala kan være nyttig. Vi begynner med et eksempel der vi kartlegger alder mot bruttoinntekt for 100 personer (i form av et punktdiagram).

Selv om man kan anta at inntekten øker med alderen, blir det vanskelig å se dette i diagrammet, fordi noen personer har langt høyere inntekter sammenlignet med majoriteten.

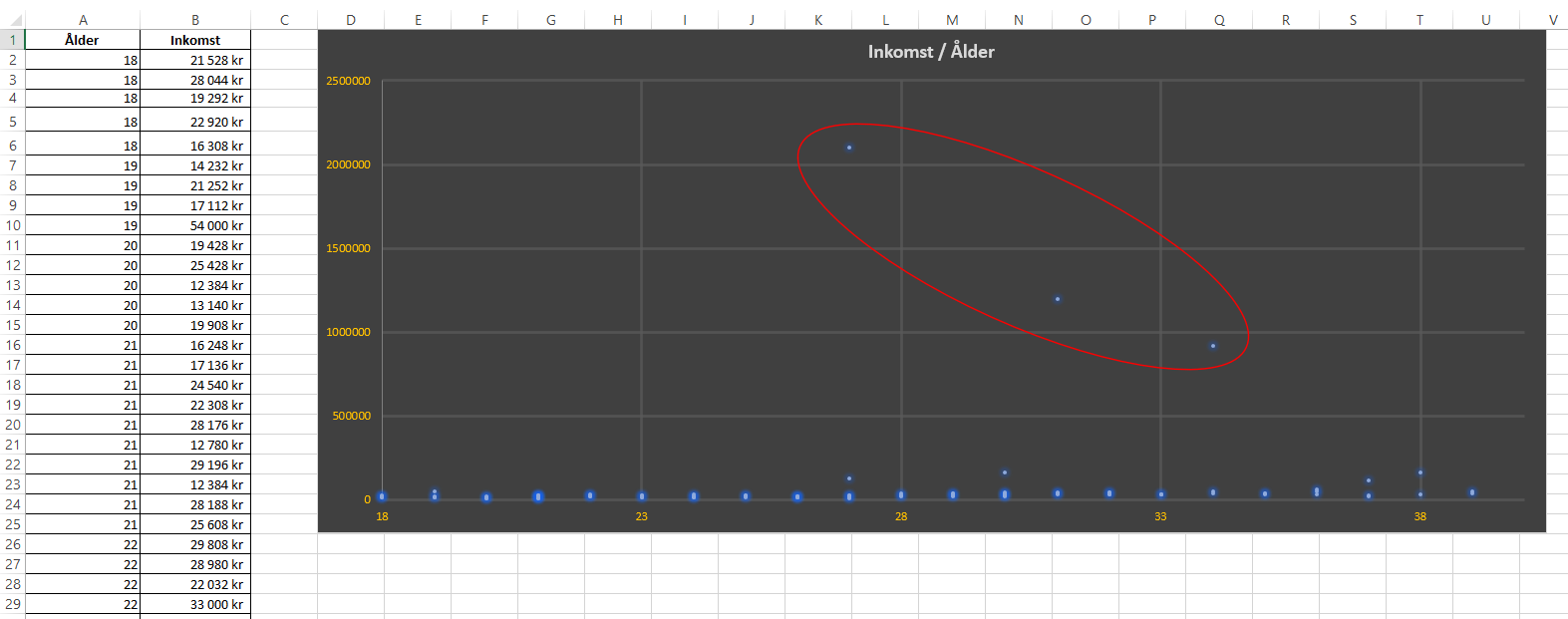
Siden hvert intervall på y-aksen er like stort, vil lavere inntekter bli komprimert i diagrammet for hvert intervall som legges til for å kunne inkludere de høyeste verdiene i dataserien.

Dette problemet kan løses ved hjelp av en logaritmisk skala. I motsetning til lineære skalaer defineres en logaritmisk skala som: forrige intervallverdi multiplisert med en basisverdi.

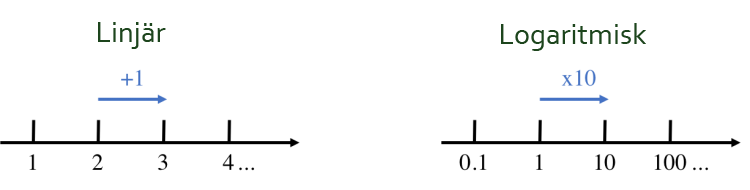
Grunnideen er altså å komprimere høye verdier for å beholde høy “oppløsning” blant lavere verdier.

>>For å endre en akse til logaritmisk i Excel, høyreklikk på aksen og velg “Formater akse“. Klikk deretter på “Logaritmisk skala” og skriv inn basisverdien.

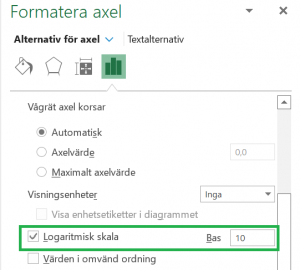
Vi ser nå at høye inntekter ligger i sine egne intervaller. Blant lavere inntekter ser vi en tydelig trend som indikerer at inntekten øker med alderen.

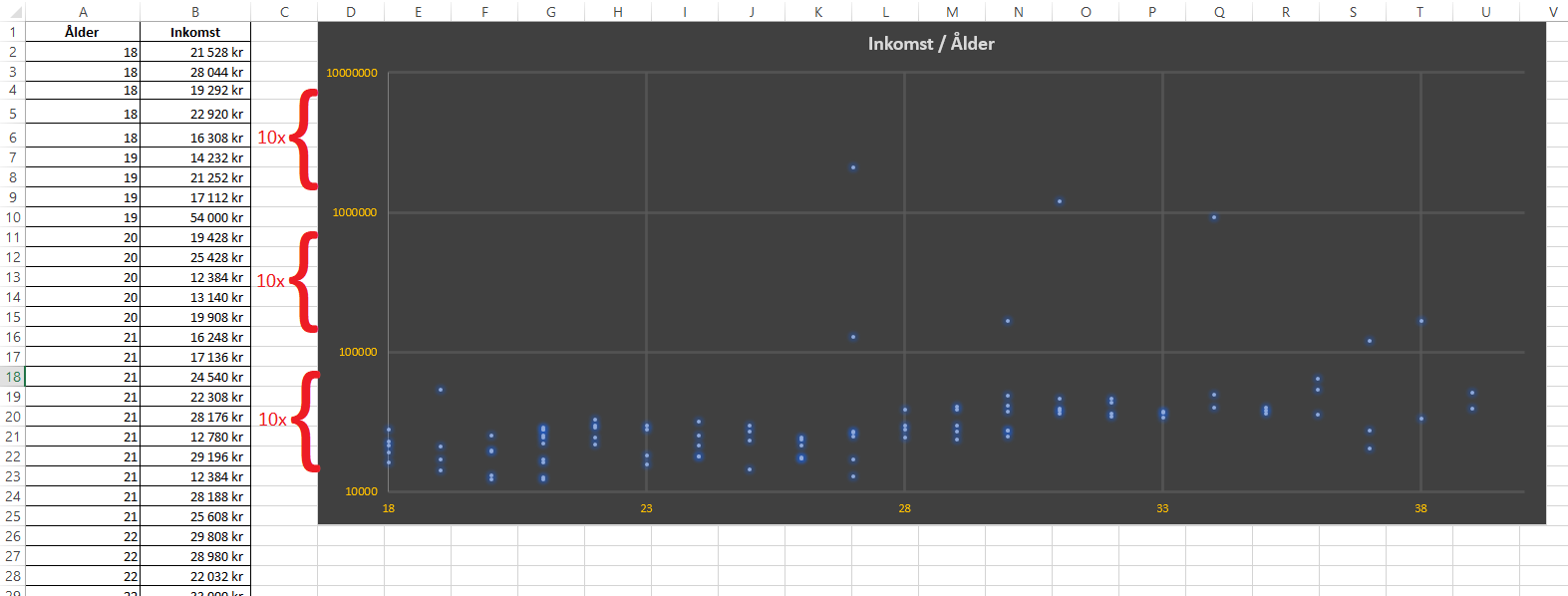
Det finnes ingen klar regel for når man bør bruke logaritmisk skala, men vanligvis brukes den av to grunner. Den første er når store verdier forvrenger grafen for resten av dataene, og den andre er for å vise multiplikative faktorer eller prosentvise endringer.

La oss se på et eksempel med prosentvis endring: hvis vi endrer basisverdien fra 10 til 2, betyr det at hvert intervall tilsvarer en økning på 100 %. Dette er spesielt nyttig dersom den prosentvise forskjellen er det som er av interesse.

Blant annet i økonomiske sammenhenger er det ikke uvanlig å betrakte f.eks. markedsindekser eller aksjepriser som prosentvise endringer.

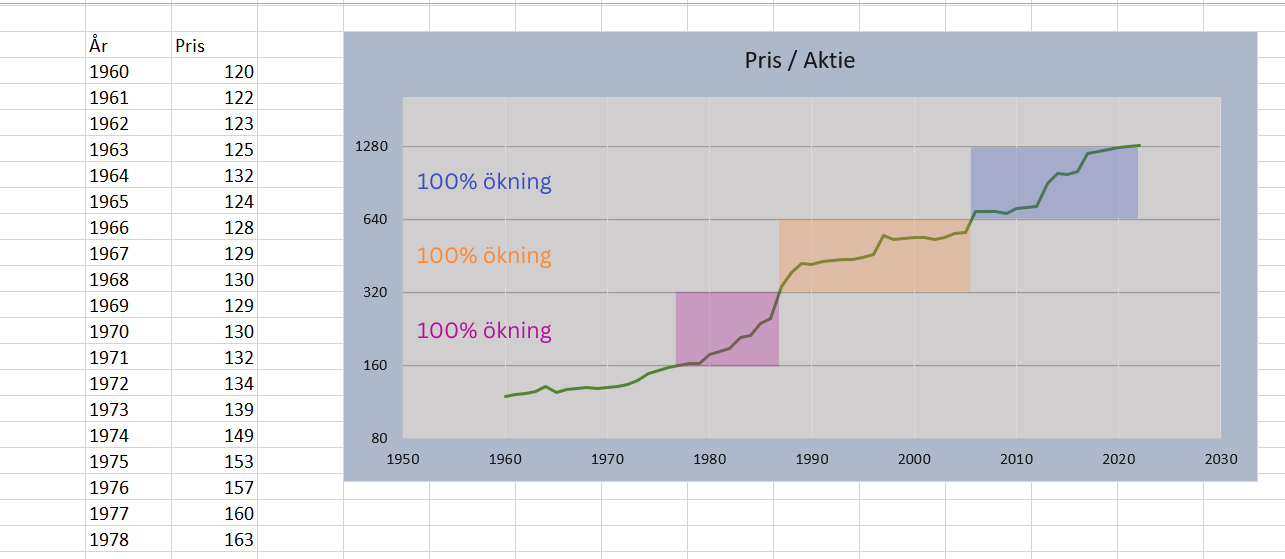
Ved å sette et minimumsverdi i diagrammet, kan vi også styre hvilket grunnverdi den logaritmiske skalaen baserer seg på.